I beaded a four-dimensional thing that I don't understand very well.
What I do know is that it's a beaded version of a 4-D Archimedean polytope that goes by many names.
It's made of different polyhedra, in the same kind of way that a polyhedron is made up of different polygons.
I learned about this structure from a book called, "The Symmetry of Things" by Conway, Burgiel, and Goodman-Strauss. You can see the various names it goes by in this photo, which is a page out of that book. This page is the direct inspiration for this beadwork. More so, it's a recipe for how all of the loops fit together.
As a mathematician, I simply beaded this recipe using beaded angle weave. Each n-gon is a loop of n beads. The arrangement of the loops is the same and the arrangement of the polygons in Conway's illustration. (However, I left out the thread to stitch the 10-gons because by the time I got to them, the beadwork didn't need or want it.)
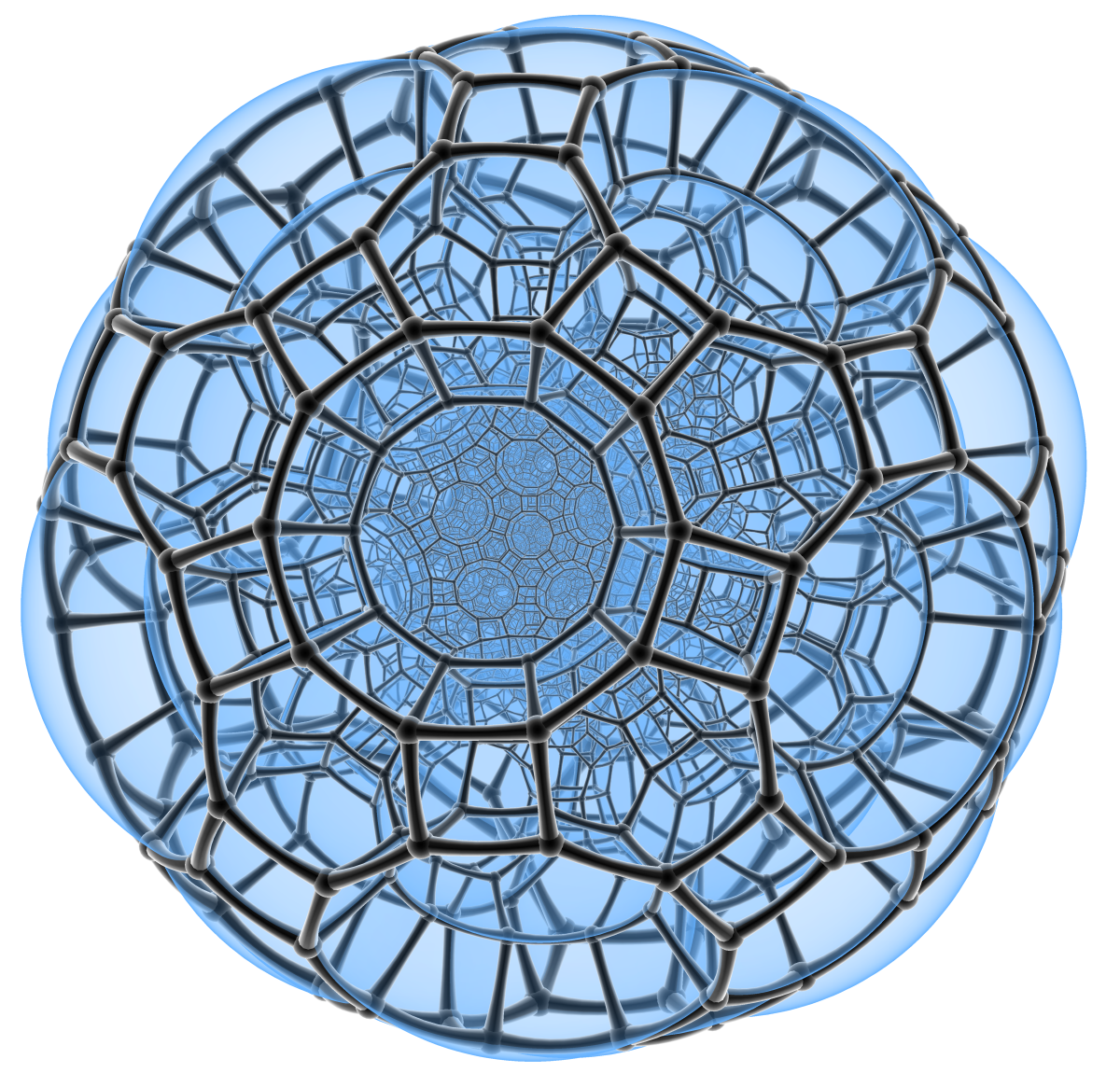
Now that it's done, I'm pretty sure what I beaded is called an omnitruncated 120-cell on Wikipedia. Fritz Obermeyer created and gifted this image into the public domain. Isn't it pretty?
This beautiful blue thing has 2640 total polyhedra:
120 4.6.10
720 4.4.10
1200 4.4.6
600 4.6.6
I didn't bead anywhere near that entire mathematical object, but I did bead a little chunk of it. In fact, I only finished one of the 120 of the (4.6.10). The weird thing about beading this object is you can just keep adding more and more loops and more and more polygons. It feels a lot like beading the infinite skew polyhedron faujasite because they share many of the same shapes connected in the same ways. However, faujasite is an infinite 3D structure, and this is a finite 4D structure. And in this thing, the angles don't work correctly in 3D. To see what I mean, look at all of the distortion in that blue image above. Everything in the center is squished, and everything near the outside is all stretched out. So you couldn't bead the whole thing the way I beaded mine here. But we can bead lots of different chunks of it. I definitely could have kept going. The challenge as an artist is to decide where to stop.
I made this beaded sculpture by weaving glass beads together with a needle and thread. It contains nearly 25 grams of chocolate bronze size 11° seed beads, which is more than a full tube. There are usually around 100 size 11° seed beads per gram; so that's about 2500 beads. I'm pretty sure it's the only one like it. This piece is very tactile and fun to turn in your hands to see all of the different views.
Largest diameter is 6 cm (2 and 3/8 inches). You could put a piece of cord through it and wear it as a large pendant, if you were so inclined. If you would like to have it, you can find it here in my Etsy shop. Thanks for looking.
What I do know is that it's a beaded version of a 4-D Archimedean polytope that goes by many names.
It's made of different polyhedra, in the same kind of way that a polyhedron is made up of different polygons.
I learned about this structure from a book called, "The Symmetry of Things" by Conway, Burgiel, and Goodman-Strauss. You can see the various names it goes by in this photo, which is a page out of that book. This page is the direct inspiration for this beadwork. More so, it's a recipe for how all of the loops fit together.
As a mathematician, I simply beaded this recipe using beaded angle weave. Each n-gon is a loop of n beads. The arrangement of the loops is the same and the arrangement of the polygons in Conway's illustration. (However, I left out the thread to stitch the 10-gons because by the time I got to them, the beadwork didn't need or want it.)
Now that it's done, I'm pretty sure what I beaded is called an omnitruncated 120-cell on Wikipedia. Fritz Obermeyer created and gifted this image into the public domain. Isn't it pretty?
This beautiful blue thing has 2640 total polyhedra:
120 4.6.10
720 4.4.10
1200 4.4.6
600 4.6.6
I didn't bead anywhere near that entire mathematical object, but I did bead a little chunk of it. In fact, I only finished one of the 120 of the (4.6.10). The weird thing about beading this object is you can just keep adding more and more loops and more and more polygons. It feels a lot like beading the infinite skew polyhedron faujasite because they share many of the same shapes connected in the same ways. However, faujasite is an infinite 3D structure, and this is a finite 4D structure. And in this thing, the angles don't work correctly in 3D. To see what I mean, look at all of the distortion in that blue image above. Everything in the center is squished, and everything near the outside is all stretched out. So you couldn't bead the whole thing the way I beaded mine here. But we can bead lots of different chunks of it. I definitely could have kept going. The challenge as an artist is to decide where to stop.
I made this beaded sculpture by weaving glass beads together with a needle and thread. It contains nearly 25 grams of chocolate bronze size 11° seed beads, which is more than a full tube. There are usually around 100 size 11° seed beads per gram; so that's about 2500 beads. I'm pretty sure it's the only one like it. This piece is very tactile and fun to turn in your hands to see all of the different views.
Largest diameter is 6 cm (2 and 3/8 inches). You could put a piece of cord through it and wear it as a large pendant, if you were so inclined. If you would like to have it, you can find it here in my Etsy shop. Thanks for looking.







That was AWESOME!!!!!
ReplyDelete